各位同学大家好，今天来聊一聊数量关系当中的溶液问题，溶液问题在数量关系当中算是比较简单一个模块，虽然简单，但类型可不少，比如说混合问题、蒸发稀释型、反复操作型，解题方法也是多种多样，那有没有比较高效而又容易上手得方法了。首先，我们得明白溶液问题最基础的公式，溶质=溶液×浓度，溶液=溶质+溶剂。不管溶液问题怎么变化，都脱离不了基础的运算公式。

　　这么多的题型分类，如果都去记公式背套路，那确实很辛苦，而且还不一定记得住，用错公式更加得不偿失，往往决定胜败的可能就是那么一分。为了更好的解决溶液问题，给大家分享一个小诀窍：“任你千变万化，我自抓住溶质死磕”。溶质是溶液问题的核心，有了溶质才有溶液，有了溶质才有浓度，所以只要抓住溶质的变化，找准等量关系，所有的溶液问题都不再是问题。来看以下几道例题。

　　例1.将300克浓度95%的酒精与若干浓度60%的酒精，混合成浓度75%的酒精，需要浓度

　　60%的酒精多少克?

　　A.225

　　B.240

　　C.380

　　D.400

　　这道题属于溶液中的混合问题，两个部分混合之后得整体溶液，两个部分的溶质也随着混合变为一个整个，所以各部分溶质相加得总溶质，以此来进行计算，通俗好懂，也好列等式：300×95%+60%×a(a为浓度为60%溶液的量)=75%×(300+a)，解得a=400,因此选D。

　　例2.现有浓度为4%的食盐水250克，若向该食盐水添加10克食盐，再蒸发掉160克水，则新获得的食盐水的浓度为：

　　A.10%

　　B.15%

　　C.20%

　　D.25%

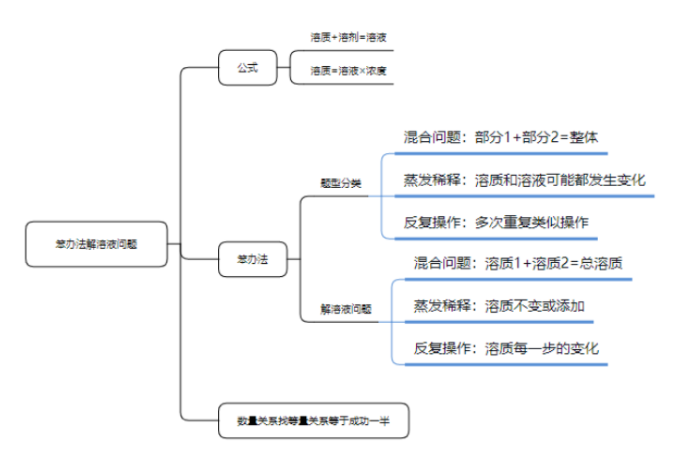
　　通过以上三道题的分析，不论是反复操作、蒸发稀释还是混合问题，把握溶质的变化，溶液问题确实可以变得很简单，希望通过今天的分享，能给辛勤备考的你带来帮助，早日圆梦公职。